the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Paramagpy: software for fitting magnetic susceptibility tensors using paramagnetic effects measured in NMR spectra
Henry William Orton
Thomas Huber
Gottfried Otting
Paramagnetic metal ions with fast-relaxing electrons generate pseudocontact shifts (PCSs), residual dipolar couplings (RDCs), paramagnetic relaxation enhancements (PREs) and cross-correlated relaxation (CCR) in the nuclear magnetic resonance (NMR) spectra of the molecules they bind to. These effects offer long-range structural information in molecules equipped with binding sites for such metal ions. Here we present the new open-source software Paramagpy, which has been written in Python 3 with a graphic user interface. Paramagpy combines the functionalities of different currently available programs to support the fitting of magnetic susceptibility tensors using PCS, RDC, PRE and CCR data and molecular coordinates in Protein Data Bank (PDB) format, including a convenient graphical user interface. Paramagpy uses efficient fitting algorithms to avoid local minima and supports corrections to back-calculated PCS and PRE data arising from cross-correlation effects with chemical shift tensors. The source code is available from https://doi.org/10.5281/zenodo.3594568 (Orton, 2019).
- Article
(1994 KB) -
Supplement
(1556 KB) - BibTeX
- EndNote
Paramagnetic metal ions with fast-relaxing electrons produce a number of spatially dependent effects in nuclear magnetic resonance (NMR) spectra of biomolecules which are useful for probing molecular structure and interactions. These effects arise from the magnetic susceptibility of unpaired electrons, which manifests in NMR spectra most notably as pseudocontact shifts (PCSs), paramagnetic relaxation enhancements (PRE) and residual dipolar couplings (RDCs), but also as cross-correlated relaxation (CCR) effects. PCSs and RDCs only arise when the magnetic susceptibility is anisotropic, which is the case for all trivalent paramagnetic lanthanide ions except Gd3+.
A number of programs have been developed for fitting the parameters of magnetic susceptibility tensors, χ, to atomic coordinates of biomolecules using the paramagnetic effects experimentally observed in NMR spectra. The program Numbat supports calculation and fitting of the magnetic susceptibility anisotropy tensor, Δχ, from experimental PCS data with corrections for residual anisotropic chemical shifts (RACSs) (John et al., 2005) in a convenient graphical user interface (GUI) (Schmitz et al., 2008). The Python module PyParaTools offers similar functionality to Numbat but in a scripting environment and adds methods for fitting χ tensors and alignment tensors using PREs and RDCs, respectively (Stanton-Cook et al., 2014). The software FANTEN offers a convenient web-based GUI for fitting Δχ and alignment tensors from PCS and RDC data sets, respectively (Rinaldelli et al., 2015).
RDCs arise not only from paramagnetism, but also in the presence of alignment media such as dilute liquid crystals. The programs PALES (Zweckstetter and Bax, 2000) and REDCAT (Valafar and Prestegard, 2004) fit alignment tensors to atomic coordinates using RDCs. The program Module can use RDCs to fit alignment tensors for molecular structure refinement (Dosset et al., 2001). PCS and RDC restraints have also been implemented in the software packages CYANA (Balayssac et al., 2006), XPLOR-NIH (Banci et al., 2004), Rosetta (Schmitz et al., 2012; Raman et al., 2010) and HADDOCK (Dominguez et al., 2003; de Vries et al., 2010) for structure determination and refinement.
The coordinates of paramagnetic centres can also be determined from PREs, and suitable fitting programs include the programs RelaxGUI (Bieri et al., 2011) and Spinach (Hogben et al., 2011). CCR effects can occur between Curie-spin and dipole–dipole relaxation (Ghose and Prestegard, 1997) and also between Curie-spin and chemical shift anisotropy (CSA) relaxation (Pintacuda et al., 2004a). The former is observed as a difference in relaxation rates between the multiplet components of scalar coupled resonances (Ghose and Prestegard, 1997; Bertini et al., 2002a). The software FANTACROSS supports calculation of this CCR effect, but does not allow fitting of the χ tensor position (Bertini et al., 2001b). The latter CCR effect was experimentally demonstrated only recently (Orton et al., 2016).
NMR spectra of biomolecules labelled with paramagnetic metal ions with fast electronic relaxation rates, as afforded by lanthanide tags, simultaneously display PCS, RDC, PRE and CCR effects in the same spectrum (Pintacuda et al., 2004b). Due to their common origin in the paramagnetism of the metal ion, all these effects are interrelated. For example, the Δχ tensor determined from PCS measurements can, in principle, be used to predict RDCs, and RDCs arising from paramagnetic alignment allow predictions of some of the Δχ-tensor parameters. The software PyParaTools offers convenient integration of all of these effects, but it lacks many refinements, such as the computation of RACS effects which may affect PCS measurements (John et al., 2005), explicit routines for calculating PREs based on Solomon–Bloembergen–Morgan (SBM) or Curie-spin relaxation theory including anisotropic effects arising from non-vanishing Δχ tensors, calculation of cross-correlated Curie-spin–CSA PRE effects or Curie-spin and dipole–dipole CCR involving anisotropic Δχ tensors, or anisotropic SBM (Suturina et al., 2018) calculations.
Here we present a new Python-based program, Paramagpy, which offers a graphical interface for fitting magnetic susceptibility tensors using PCS, RDC, PRE and CCR data and seamless transition between these calculations. The fitting routine of Paramagpy for determining Δχ tensors from PCSs employs an efficient grid search algorithm as previously implemented in GPS-Rosetta (Schmitz et al., 2012). The algorithm is adept at overcoming the local minima problem that sometimes compromises the results obtained with Numbat and PyParaTools. Paramagpy uses both Curie-spin (Guéron, 1975) and Solomon–Bloembergen–Morgan (Solomon, 1955) theory to calculate PREs, and it includes cross-correlation effects with anisotropic chemical shift tensors (Pintacuda et al., 2004a), which have not been taken into account by any previous tensor-fitting software. Paramagpy can be installed as a Python module and scripted for efficient calculations, or run via an intuitive GUI.
Calculations using Paramagpy have been verified with data from previous publications. This includes fitting of Δχ tensors to amide PCS data of lanthanide-loaded calbindin D9k and calculating PREs for amide 1H spins (Orton and Otting, 2018). Paramagpy has also been used successfully to predict cross-correlated CSA–Curie-spin relaxation giving rise to negative PREs for amide 15N spins (Orton et al., 2016). CCR calculations have been verified with data from high- and low-spin paramagnetic myoglobin (Pintacuda et al., 2003). Paramagpy has been shown to fit alignment tensors consistent with previous results for lanthanide-tagged ubiquitin (Pearce et al., 2017), but may also be applied to data sets arising from alignment media where Paramagpy reports alignment and Saupe tensors alongside Δχ tensors. Paramagpy can thus be used with RDC data obtained by any means of weak molecular alignment in the magnetic field, substituting software like Module (Dosset et al., 2001).
The magnetic susceptibility tensor χ associated with a paramagnetic centre creates a dipolar shielding tensor σ at a given position r and distance r from the paramagnetic centre as shown in Eq. (1), where I3 is the 3×3 identity matrix, ⊗ denotes the Kronecker product and . denotes the matrix multiplication.
The PCS is given by the trace of the shielding tensor as shown in the PCS Eq. (3). The Δχ tensor is given by the traceless part of the χ tensor. Considering only the Δχ tensor, a linear form of the PCS equation can be obtained, which characterises the Δχ tensor by five explicit parameters as shown in Eq. (4). Including the three position parameters represented by the coordinates of the metal centre (x, y, z), solving the PCS equation requires determining eight parameters in total.
2.1 Singular value decomposition (SVD) grid search
Equation (4) can be rewritten in matrix form to give Eq. (5), where b is a column vector of length n of the calculated PCS values, x is a column vector of length 5 of the Δχ-tensor parameters and A is a n×5 matrix with rows defined by the row vector in Eq. (4) containing coordinate parameters.
Populating vector b with many experimental PCS values and the matrix A with atomic coordinates from a molecule of known structure, the system is likely overdetermined and a least-squares solution for the Δχ-tensor parameters x can be obtained analytically by considering the singular values of the matrix A and constructing the pseudo-inverse A+. This allows calculation of the best-fitting tensor at a given position by Eq. (6) (Schmitz et al., 2012). A weighted least-squares fit can be obtained using Eq. (7), where the square matrix W contains the weights along the diagonal , which may be sourced from the experimental standard deviations SPCS,i of the ith spin.
Since this calculation is fast, a grid search over many positions of the paramagnetic centre is feasible, providing a robust initial guess prior to iterative refinement of the tensor position by non-linear gradient-descent methods. Paramagpy can evaluate 5000 grid points for 50 PCS values in under 1 s using a 2 GHz Intel i5 2016 processor of a typical laptop computer.
2.2 Non-linear gradient descent
When fitting of the position of the paramagnetic centre is required, the PCS equation becomes non-linear. A fit can be found iteratively by minimising the sum of squares of the differences between experimental and back-calculated PCS values. An efficient method for minimisation is by non-linear gradient descent. We chose the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm (Fletcher, 1988) for non-linear least-squares minimisation of the cost function in Eq. (8). Here, and are, respectively, the experimental and back-calculated PCSs for spin i, and SPCS,i is the experimental uncertainty in the PCS of spin i.
2.3 Multiple PCS data sets
Often there are multiple PCS data sets available for different metal ions bound at the same position, obtained from multiple samples prepared with different metal ions. A simultaneous fit of the common position is possible, independently fitting the tensor magnitude and orientation for each data set, and can lead to a more accurate overall position of the paramagnetic centre. Paramagpy supports multiple data sets for simultaneous fitting of a common metal position by both the SVD grid-search and non-linear gradient-descent algorithms.
2.4 Corrections to PCS calculations
An anisotropic magnetic susceptibility causes alignment of the molecule in the external magnetic field. As molecular orientations are no longer sampled uniformly, shielding tensors may no longer average to their isotropic values. In this situation, the chemical shift actually observed in the paramagnetic sample contains contributions from residual anisotropic chemical shifts (RACSs) arising from non-zero averaging of the chemical shift anisotropy (CSA) tensor. Paramagpy supports PCS calculations that include RACS corrections (John et al., 2005). Paramagpy provides standard CSA tensors for amide 1H spins and backbone amide 15N and carbonyl 13C spins (Cornilescu and Bax, 2000). Customised CSA tensors may also be set for any of the nuclear spins.
In addition to the CSA tensor, there is also a dipolar shielding tensor σ at the site of a nuclear spin, which arises from the magnetic susceptibility of the paramagnetic centre. In analogy to the RACS effect, this can lead to a residual anisotropic dipolar shift (RADS), which is a small perturbation to the observed PCS in paramagnetic samples arising from molecular alignment (Bertini et al., 2002b). Paramagpy includes RADS as an option in the PCS calculation and Δχ-tensor fitting routines.
Systematic errors in experimental PCS values can arise due to variations in the carrier frequency or calibration of the recorded NMR spectra of the diamagnetic and paramagnetic species. This offset can be included as a parameter during the fitting of Δχ tensors, although doing so is meaningful only if a sufficient number of PCS data are available to avoid overfitting.
An anisotropic magnetic susceptibility tensor induces a coincident alignment tensor A, giving rise to RDCs between nuclear spins. The alignment tensor can be found from the Δχ tensor using Eq. (9), where B0 is the magnetic field, μ0 the vacuum permeability, kB the Boltzmann constant and T the temperature (Bertini et al., 2002b).
The RDC values can be calculated using Eq. (10), where rAB is the internuclear vector and rAB the distance between the two nuclei A and B (Kramer et al., 2004). This can be expanded into the vector equation Eq. (11), where x, y and z are the Cartesian coordinates of the internuclear vector rAB.
Unlike the PCS tensor, the RDC tensor does not require parameters for position and can therefore be described by five parameters for magnitude and orientation. Fitting can therefore be achieved by a linear least-squares fit.
3.1 SVD fitting algorithm
Paramagpy uses the SVD algorithm similar to the original implementation in the program REDCAT (Valafar and Prestegard, 2004). It is functionally the same as the algorithm applied to solving the PCS equation in Sect. 2.1. A n×5 matrix with rows defined by the row vector in Eq. (11) containing coordinate parameters is constructed. From this, a pseudo-inverse matrix is calculated and applied to the experimental RDC values, yielding the best-fitting alignment tensor.
PREs describe the relaxation rates of longitudinal magnetisation, , or transverse magnetisation, , of nuclear spins, where T1 and T2 are the longitudinal and transverse relaxation times, respectively. For PREs of paramagnetic molecules in solution, the relaxation rates are governed by dipole–dipole interactions as described by the SBM equations or the shielding tensor anisotropy as described by the Curie-spin equations (Solomon, 1955; Guéron, 1975).
4.1 Solomon–Bloembergen–Morgan theory
The SBM equations for R1 and R2 are shown in Eqs. (12) and (13), respectively, where γ is the nuclear gyromagnetic ratio, r the distance of the nucleus from the paramagnetic centre, and ω and ωS the nuclear and electronic Larmor frequencies, respectively. τc is the correlation time calculated as , where τr is the rotational correlation time of the molecule and T1e is the electronic relaxation time. μeff is the effective magnetic moment of the paramagnetic centre, which can be predicted from the Landé g factor, the Bohr magneton μB and the total angular momentum quantum number J (Eq. 14).
An extension to the SBM theory which accounts for anisotropy of the dipolar spectral density is described by Eqs. (15) and (16) where G(ω) describes the spectral power density tensor (Suturina et al., 2018). is the unit vector from the paramagnetic centre to the nuclear spin. The spectral power density tensor usually cannot be derived theoretically, but is instead fitted to experimental data.
4.2 Curie-spin theory
Curie-spin relaxation is governed by the dipolar shielding tensor σ as calculated in Eq. (1), which must include the isotropic component of the χ tensor, χiso, which can be predicted using Eq. (17). The first invariant Λ and second invariant Δ of the shielding tensor are calculated by Eqs. (18) and (19), where σij denotes the ith and jth components of the shielding tensor σ (Suturina et al., 2018). This allows calculation of the R1 and R2 PREs by Eqs. (20) and (21), respectively. These equations account for anisotropy of the magnetic susceptibility, provided Eq. (1) is used to calculate σ (Vega and Fiat, 1976).
When PREs due to Curie-spin relaxation are cross-correlated with CSA relaxation, the CSA tensor is added to the dipolar shielding tensor to give an effective shielding tensor σeff. The PRE including CSA cross-correlation RCurie × CSA is determined as the difference in relaxation rates in the paramagnetic and diamagnetic state as shown in Eq. (22). This can give rise to negative PREs as shown previously and confirmed by experiment (Pintacuda et al., 2004a; Orton et al., 2016).
4.3 Fitting algorithm
Paramagpy includes routines to calculate PREs and fit all parameters for each of the above relaxation theories, including cross-correlated relaxation with CSA effects. This is achieved by non-linear gradient descent to minimise the cost function of Eq. (23). Here, and are, respectively, the experimental and back-calculated PREs for spin i, and SPRE,i is the experimental uncertainty in the PRE of spin i. The user can choose to fit or constrain different parameters, such as the magnetic susceptibility or power spectral density tensor position, magnitude, correlation time τc, etc. Parameter templates for lanthanide ions are also provided, based on tensor magnitudes and anisotropies previously reported for lanthanide complexes of calbindin D9k (Bertini et al., 2001a). These may be used to give a quick estimate of expected PRE values.
Interference of the internuclear dipole–dipole (DD) relaxation with Curie-spin relaxation provides a mechanism for differential relaxation rates of multiplet components by cross-correlated relaxation (CCR) (Ghose and Prestegard, 1997). This effect is readily observed and measured as the difference in the relaxation rate R2 of the two doublet components of an amide 1H−15N spin pair. In this case, the shielding tensor arising at the 1H spin due to the 15N dipole is given by Eq. (24), where rHN is the H−N bond vector, rHN is the internuclear distance, γN is the gyromagnetic ratio of 15N and is the spin of 15N. The factor of 1∕B0 is necessary to express the 15N shielding tensor in units of parts per million to match the units of the Curie-spin shielding tensor. The effective shielding tensor for the 1H spin due to both the Curie spin and the 15N dipole in either the up or down spin state is given by Eqs. (25) and (26), respectively. The relaxation rate is then calculated using Eq. (21) for both the up and down effective shielding tensors σ↑ and σ↓, and their difference is taken to represent the Curie × DD differential line broadening RCurie × DD. In this way the auto-correlated relaxation mechanisms arising from the separate DD and Curie mechanisms are subtracted out, leaving the pure cross-correlated term. A derivation showing the equivalence of Eqs. (24)–(27) to those reported by Ghose and Prestegard (Ghose and Prestegard, 1997) is given in the Supplement.
Paramagpy uses the above equations for all DD × Curie relaxation calculations. By using Eq. (1) for calculating the Curie-spin shielding tensor σ, these equations also account for anisotropy of the magnetic susceptibility χ. CCR values can be calculated between any two atoms in the specified Protein Data Bank (PDB) file. The calculations have been shown to agree with previous experimental CCR data on high- and low-spin myoglobin (Pintacuda et al., 2003).
5.1 Fitting algorithm
Paramagpy includes routines to fit all parameters of the χ tensor, including position, magnitude and anisotropy, to experimentally measured CCR data. This is achieved by non-linear gradient descent to minimise the cost function of Eq. (28). Here, and are, respectively, the experimental and back-calculated CCRs for spin i, and SCCR,i is the experimental uncertainty in the CCR of spin i.
To judge the quality of a Δχ or χ tensor fitted using PCS, RDC, PRE or CCR data, Paramagpy offers three methods to test the robustness of the fit: structure-sourced, bootstrap and Monte Carlo. The structure-sourced method assumes that multiple models in a PDB file represent experimental uncertainty in the atomic coordinates as is common for NMR structures (see Sect. 7.1). In this approach, a tensor is fitted to each individual model and uncertainties in the fitted tensor parameters are reported. The alternative bootstrapping method repeats the fit many times, with each iteration randomly sampling a specified proportion of the data, and subsequently reports the standard deviation in the fitted tensor parameters. The Monte Carlo method repeats the fit using all the data, but each time adds noise to the experimental values. The noise is sourced from a uniform distribution that has been scaled by values provided by the user for each atom. These scaling values are ideally calculated from noise in the spectrum to reflect uncertainty in peak positions or amplitudes (Kontaxis et al., 2000). The standard deviations in the fitted tensor parameters are then reported.
7.1 Structures with uncertainties represented by a family of models
Biomolecular structures in the PDB, which have been determined by solution NMR, usually report experimental uncertainty in the atomic coordinates by including multiple models, which individually fulfil the experimental restraints. The default behaviour of Paramagpy is to fit a magnetic susceptibility tensor to each model independently and then report an average of all these tensors. The tensor averaging is achieved by Eq. (29) where the summation runs over the tensors fitted to each of the n models. This ensures no errors are introduced by averaging prolate/oblate tensors with different principal axis definitions. All other parameters involved in the fit, such as origin of the tensor position, rotational correlation time or electronic relaxation time, are averaged in the conventional way. Note that the final result is sensitive to different relative orientations of the models.
7.2 Structures represented by a conformational ensemble
Some coordinate sets in the PDB have been determined by molecular dynamics, where the ensemble of models deposited fulfils the experimental restraints better than each individual model. For this case, Paramagpy has the option for calculation of ensemble-averaged paramagnetic effects at all stages of calculations and fitting. Ensemble-averaged fitting presents a subtle but important difference compared to the multiple-model method described in Sect. 7.1 above. This is particularly noticeable for RDCs, where the ensemble average can be much smaller than the corresponding RDC of a single model, and therefore several models representing different bond orientations may be simultaneously required to fit an appropriate alignment tensor or Δχ tensor.
The implementation of ensemble averaging in Paramagpy averages the paramagnetic values calculated for each atom in the different models, identifying the specific atoms by identical atom numbers in the PDB file. Custom ensemble averaging behaviour can be changed by the user in the scripted environment. In the implementations of the SVD algorithm, ensemble averaging involves summation of rows for common atoms of the matrix A of Eq. (5) before calculation of the singular values. In the implementations of the non-linear gradient descent algorithm, the values calculated for the common atoms are averaged prior to calculating the sum of squares of differences. This is shown in Eq. (30) where acal and aexp are the calculated and experimental PCS, RDC, PRE or CCR values, respectively. The index m is for atoms that are common between models, and the index i runs over all atoms in the structure.
7.3 Fitting tensor parameters to multimers
In the case of symmetric multimers composed of monomers with each containing a paramagnetic metal ion, the ensemble averaging feature of Paramagpy can be exploited to fit the Δχ tensor associated with a given monomer. This is achieved simply by defining the monomeric units in the PDB file as models of the same structure and applying the ensemble averaging routine to fit the Δχ tensor using the experimental PCSs, which reflect the average of the PCSs observed in each monomer. Note that, due to the averaging, the final fitted Δχ tensor must be scaled by the user n-fold, where n is the number of monomers. This feature can also be exploited in NMR crystallography (Kervern et al., 2009).
To judge the agreement of tensor fits with the experimental data, a Q factor can be assigned to a given fit, which Paramagpy calculates using Eq. (31). Here, the experimental and calculated PCS, RDC, PRE or CCR values are denoted aexp and acal, respectively, the index m is for ensemble averaging of common spins between models, and the index i is for summation over all spins of the molecule. A low Q factor signifies a good-quality fit.
Alternative Q factors have been proposed (Clore and Garrett, 1999; Bashir et al., 2010). The Q factor proposed by Bashir et al. (2010), which uses sums of experimental and calculated values in the denominator of Eq. (31) and therefore tends to be 2 times smaller, is supported by the scripted environment of Paramagpy. It is important to note that the fitting algorithm used by Paramagpy targets the minimal root-mean-square deviation between experimental and calculated data rather than the Q factor. It has been pointed out that Q-factor evaluations are meaningful only if the number of fitted data greatly exceeds the number of variables (Bax, 2003).
Paramagpy has a graphical user interface (GUI) written for the inbuilt Tk/Tcl interface of Python 3, which can run on Mac OS X, Windows and Linux operating systems. The GUI offers a user-friendly environment for loading and visualising PDB files and experimental PCS, RDC, PRE and CCR data. Two frames display the initial and fitted tensors. The fitted tensor is calculated and displayed by the push of a button. An overview of the PCS fitting tab is shown in Fig. 1. Hovering the mouse over any element in the window displays a useful tool tip to help the user.
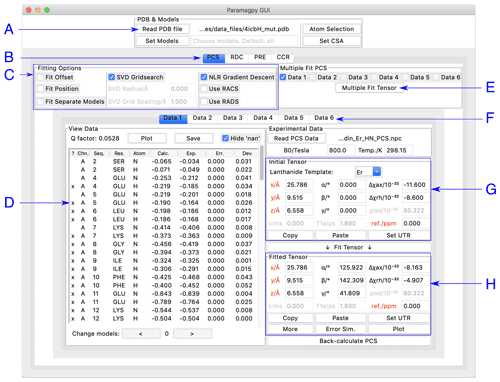
Figure 1Paramagpy GUI running on Mac OS X. (A) Frame for loading PDB coordinates. The atoms and models (conformers) of interest can be selected and CSA-tensor parameters set by the user. (B) The user can switch between PCS, RDC, PRE and CCR tabs, where CCR stands for the Curie-spin–dipole–dipole cross-correlated relaxation. (C) Fitting options can be specified by selecting the relevant check box. The “SVD Gridsearch” option searches for the best-fit tensor within a sphere about the initial tensor origin with radius and grid spacing as specified. The “NLR Gradient Descent” option refines the tensor using non-linear least-squares minimisation. (D) Experimental data for atoms in the PDB file are displayed here. The first column contains an “x” if the datum will be used during fitting and may be toggled by pressing the “x” key on the keyboard. Experimental and back-calculated PCS values are also reported and their correlation can be displayed by clicking the “Plot” button above. (E) To utilise multiple PCS data sets to fit different tensors to a common position, the “Multiple Fit Tensor” button can be clicked after selecting the desired data sets. (F) Each tab can contain a different PCS data set, allowing up to 6 to be loaded. If more data sets are required, Paramagpy supports this through the scripted module. (G) The initial tensor parameters can be specified here to define a starting point before fitting. For convenience, the paramagnetic centre can be positioned at any atom in the PDB file by double-clicking on a row of the data view in the frame to the left. Parameters in red are constrained during fitting. Greyed out parameters are not relevant to PCS or RDC calculations, but are used in PRE and CCR calculations. (H) The fitted tensor is displayed here. Clicking the “Copy” button allows the tensor to be pasted into other tabs of the program (see B and F above). The “Plot” button will prompt the user to save an isosurface file for opening in PyMOL. “Error Sim.” will assess the quality of the fit by bootstrap or Monte Carlo methods. The button “Set UTR” is for conversion of the tensor parameters to the unique tensor representation defined by the program Numbat (Schmitz et al., 2008).
Paramagpy offers a number of plot options to quickly visualise tensors and quality of fit. The scalar PCS or PRE field can be written to a CCP4 (McNicholas et al., 2011) density map, which can then be visualised as a three-dimensional contour plot in the program PyMOL (Schrödinger, LLC, 2015). The fit quality can be visualised in correlation plots of back-calculated PCS, RDC, PRE and CCR values versus the experimental values. Finally, a scatter plot of the principle axes of the tensors can be viewed in a Sanson–Flamsteed-style projection following Monte Carlo or bootstrap error analyses. Example plots are summarised in Fig. 2.
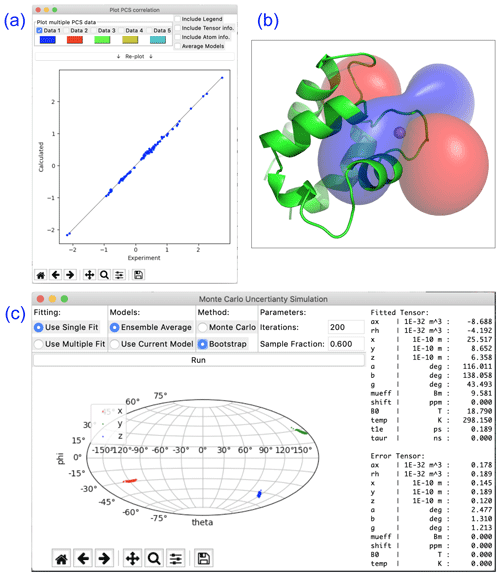
Figure 2Plotting options available in Paramagpy illustrated with data of calbindin D9k loaded with Er3+. (a) Correlation plot of calculated versus experimental PCS values after fitting of the Δχ tensor. (b) PCS isosurface plot viewed in PyMOL. (c) Sanson–Flamsteed plot showing the principle axes projections after bootstrap analysis. “Error Tensor” reports the standard deviation in fitted parameters.

Figure 3Example Python script for fitting a Δχ tensor to experimental PCS data. The output with fitted tensor parameters is displayed to the right.
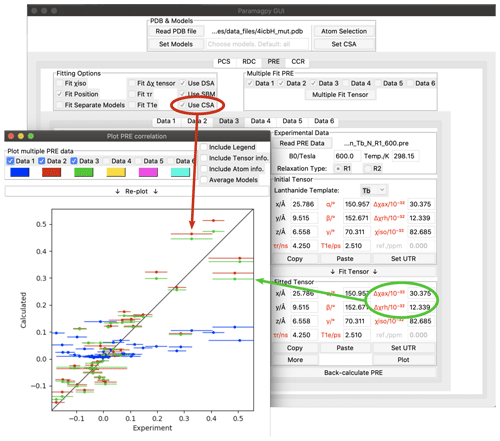
Figure 4Paramagpy GUI showing R1(15N) PRE data for calbindin D9k loaded with Tb3+. The correlation plot shows calculated vs. experimental values. Blue: SBM and isotropic Curie-spin theory are used for calculating PREs (Q factor 1.01). Red: also taking into account the cross-correlation between Curie-spin and CSA relaxation (Q factor 0.49). Green: including the additional correction arising from the anisotropy of the χ tensor (Q factor 0.47).
Paramagpy is a Python module and can be imported into a scripting environment. The module is split into four major submodules. (i) The “metal” submodule deals with the paramagnetic centre, tensor representations and methods for calculating PCS, RDC, PRE and CCR values. (ii) The “protein” submodule handles the atomic coordinates from the PDB file and CSA-tensor definitions. (iii) The “dataparse” submodule manages the reading and writing of data files. (iv) The “fit” submodule contains functions for fitting tensors to experimental data. An example script for fitting of a Δχ tensor to experimental PCS data for calbindin D9k is shown in Fig. 3. It uses only nine lines of code. Some more advanced features of Paramagpy, such as fitting of power spectral density tensors in Eqs. (15) and (16), are only available in the scripted environment. The scripted environment also offers control over which parameters are included for fitting routines and allows calculations for coordinates other than PDB formats.
Paramagpy includes macro scripts to interface with popular NMR software: CcpNmr analysis and Sparky (Vranken et al., 2005; Lee et al., 2014). Currently, these macros allow for the rapid calculation of experimental PCS values from NMR spectra with up to three dimensions, fitting of Δχ tensors and plotting of back-calculated PCS values onto paramagnetic spectra.
Paramagpy offers a number of simple routines to convert between tensor representations. In addition to the 3×3 matrix representations of tensors, positions, rotation matrices, eigenvalues, axial/rhombic components and Euler angles, alignment tensors and Saupe tensors are available upon clicking the “More” button within the GUI. The axial and rhombic components are defined as follows (Eqs. 32 and 33).
By default, Paramagpy reports all fitted tensors in the unique tensor representation used by the program Numbat (Schmitz et al., 2008). This requires that the principle axis magnitudes of the Δχ tensor are ordered , and all Euler angles are in the range [0,π] using the ZYZ convention.
PRE calculations that include anisotropy effects and cross-correlation with CSA can be daunting to set up as they require the Δχ and CSA tensors to possess the correct orientations in the frame of the molecular coordinates. Paramagpy simplifies this for the user by allowing Δχ tensors fitted from PCS data to be transferred easily to the tab for PRE calculations. Furthermore, CSA-tensor templates are provided for most protein backbone atoms.
As an example, Fig. 4 shows the Paramagpy GUI with R1(15N) PRE data for calbindin D9k loaded with Tb3+ (Orton et al., 2016). A Δχ tensor was fitted using the PCS tab, then transferred to the PRE tab using the “Copy” and “Paste” buttons. Curie-spin–CSA cross-correlation is taken into account simply by checking the box “Use CSA”. This greatly improves the correlation and allows the prediction of negative PREs, resulting in a reduction in the Q factor from 1.01 to 0.49. The small additional correction arising from the anisotropy of the Curie spin can be included by setting the Δχax and Δχrh parameters to the non-zero values obtained from the Δχ tensor fitted with the help of PCS data yielding a further reduction in the Q factor to 0.47.
The CSA tensors of 15N spins are much larger than those of 1H spins, so that Curie-spin–CSA cross-correlation effects can dominate the PRE to the point that even negative PREs can be observed (Orton et al., 2016 Fig. 4). These CCR effects are predicted to be most pronounced for 15N spins located about 10 Å from the metal ion. In contrast, the CSA of 1H spins is much smaller, so that their CCR effects are predicted to be most significant in the range of 20–25 Å and therefore too small to be easily observed experimentally (Pintacuda et al., 2004a).
Paramagpy is an easy-to-use program that integrates the related paramagnetic NMR phenomena of PCS, RDC, PRE and CCR. Paramagpy allows the rapid analysis of NMR spectra of samples containing a single paramagnetic centre, which is particularly useful for data recorded with different paramagnetic lanthanide ions. With an intuitive calculation flow, Paramagpy can be used, for example, to fit a Δχ tensor using experimental PCS data and then quickly report the expected PREs of the same complex, informing the user which signals may be too broad to observe. Paramagpy uses efficient fitting algorithms and an up-to-date implementation of paramagnetic NMR theory to capture subtle corrections arising from CSA and anisotropy effects in the PCS and PRE calculations.
The source code for Paramagpy is available at: https://doi.org/10.5281/zenodo.3594568 (Orton, 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/mr-1-1-2020-supplement.
HWO initiated the project, wrote the source code and the documentation for Paramagpy, and drafted the manuscript. GO and TH contributed advice towards code design and the final versions of the manuscript.
The authors declare that they have no conflict of interest.
Henry William Orton thanks the Westpac Bicentennial foundation for a Future Leaders Scholarship.
This research has been supported by the Australian Research Council, including a Laureate Fellowship (project no. FL170100019) to Gottfried Otting.
This paper was edited by Mikael Akke and reviewed by Marcellus Ubbink and one anonymous referee.
Balayssac, S., Bertini, I., Luchinat, C., Parigi, G., and Piccioli, M.: 13C direct detected NMR increases the detectability of residual dipolar couplings, J. Am. Chem. Soc., 128, 15042–15043, https://doi.org/10.1021/ja0645436, 2006. a
Banci, L., Bertini, I., Cavallaro, G., Giachetti, A., Luchinat, C., and Parigi, G.: Paramagnetism-based restraints for Xplor-NIH, J. Biomol. NMR, 28, 249–261, https://doi.org/10.1023/B:JNMR.0000013703.30623.f7, 2004. a
Bashir, Q., Volkov, A. N., Ullmann, G. M., and Ubbink, M.: Visualization of the encounter ensemble of the transient electron transfer complex of cytochrome c and cytochrome c peroxidase, J. Am. Chem. Soc., 132, 241–247, https://doi.org/10.1021/ja9064574, 2010. a, b
Bax, A.: Weak alignment offers new NMR opportunities to study protein structure and dynamics, Protein Sci., 12, 1–16, https://doi.org/10.1110/ps.0233303, 2003. a
Bertini, I., Janik, M. B. L., Lee, Y.-M., Luchinat, C., and Rosato, A.: Magnetic susceptibility tensor anisotropies for a lanthanide ion series in a fixed protein matrix, J. Am. Chem. Soc., 123, 4181–4188, https://doi.org/10.1021/ja0028626, 2001a. a
Bertini, I., Kowalewski, J., Luchinat, C., and Parigi, G.: Cross correlation between the dipole–dipole interaction and the Curie spin relaxation: the effect of anisotropic magnetic susceptibility, J. Magn. Reson., 152, 103–108, https://doi.org/10.1006/jmre.2001.2378, 2001b. a
Bertini, I., Cavallaro, G., Cosenza, M., Kümmerle, R., Piccioli, M., and Poggi, L.: Cross correlation rates between Curie spin and dipole-dipole relaxation in paramagnetic proteins: the case of Cerium substituted calbindin D9k, J. Biomol. NMR, 23, 115–125, https://doi.org/10.1023/A:1016341507527, 2002a. a
Bertini, I., Luchinat, C., and Parigi, G.: Magnetic susceptibility in paramagnetic NMR, Prog. Nucl. Mag. Res. Sp., 40, 249–273, https://doi.org/10.1016/S0079-6565(02)00002-X, 2002b. a, b
Bieri, M., d'Auvergne, E. J., and Gooley, P. R.: relaxGUI: a new software for fast and simple NMR relaxation data analysis and calculation of ps-ns and µs motion of proteins, J. Biomol. NMR, 50, 147–155, https://doi.org/10.1007/s10858-011-9509-1, 2011. a
Clore, G. M. and Garrett, D. S.: R-factor, free R, and complete cross-validation for dipolar coupling refinement of NMR structures, J. Am. Chem. Soc., 121, 9008–9012, https://doi.org/10.1021/ja991789k, 1999. a
Cornilescu, G. and Bax, A.: Measurement of proton, nitrogen, and carbonyl chemical shielding anisotropies in a protein dissolved in a dilute liquid crystalline phase, J. Am. Chem. Soc., 122, 10143–10154, https://doi.org/10.1021/ja0016194, 2000. a
de Vries, S. J., van Dijk, M., and Bonvin, A. M. J. J.: The HADDOCK web server for data-driven biomolecular docking, Nat. Protoc., 5, 883–897, https://doi.org/10.1038/nprot.2010.32, 2010. a
Dominguez, C., Boelens, R., and Bonvin, A. M. J. J.: HADDOCK: a protein-protein docking approach based on biochemical or biophysical information, J. Am. Chem. Soc., 125, 1731–1737, https://doi.org/10.1021/ja026939x, 2003. a
Dosset, P., Hus, J.-C., Marion, D., and Blackledge, M.: A novel interactive tool for rigid-body modeling of multi-domain macromolecules using residual dipolar couplings, J. Biomol. NMR, 20, 223–231, https://doi.org/10.1023/A:1011206132740, 2001. a, b
Fletcher, R.: Practical methods of optimization, John Wiley & Sons, New York, 2nd edn., https://doi.org/10.1002/9781118723203, 1988. a
Ghose, R. and Prestegard, J. H.: Electron spin–nuclear spin cross-correlation effects on multiplet splittings in paramagnetic proteins, J. Magn. Reson., 128, 138–143, https://doi.org/10.1006/jmre.1997.1227, 1997. a, b, c, d
Guéron, M.: Nuclear relaxation in macromolecules by paramagnetic ions: a novel mechanism, J. Magn. Reson., 19, 58–66, https://doi.org/10.1016/0022-2364(75)90029-3, 1975. a, b
Hogben, H., Krzystyniak, M., Charnock, G., Hore, P., and Kuprov, I.: Spinach – a software library for simulation of spin dynamics in large spin systems, J. Magn. Reson., 208, 179–194, https://doi.org/10.1016/j.jmr.2010.11.008, 2011. a
John, M., Park, A. Y., Pintacuda, G., Dixon, N. E., and Otting, G.: Weak alignment of paramagnetic proteins warrants correction for residual CSA effects in measurements of pseudocontact shifts, J. Am. Chem. Soc., 127, 17190–17191, https://doi.org/10.1021/ja0564259, 2005. a, b, c
Kervern, G., D'Aléo, A., Toupet, L., Maury, O., Emsley, L., and Pintacuda, G.: Crystal-structure determination of powdered paramagnetic lanthanide complexes by proton NMR spectroscopy, Angew. Chem. Int. Edit., 48, 3082–3086, https://doi.org/10.1002/anie.200805302, 2009. a
Kontaxis, G., Clore, G., and Bax, A.: Evaluation of cross-correlation effects and measurement of one-bond couplings in proteins with short transverse relaxation times, J. Magn. Reson., 143, 184–196, https://doi.org/10.1006/jmre.1999.1979, 2000. a
Kramer, F., Deshmukh, M., Kessler, H., and Glaser, S.: Residual dipolar coupling constants: an elementary derivation of key equations, Concepts Magn. Reso. A, 21, 10–21, https://doi.org/10.1002/cmr.a.20003, 2004. a
Lee, W., Tonelli, M., and Markley, J. L.: NMRFAM-SPARKY: enhanced software for biomolecular NMR spectroscopy, Bioinformatics, 31, 1325–1327, https://doi.org/10.1093/bioinformatics/btu830, 2014. a
McNicholas, S., Potterton, E., Wilson, K. S., and Noble, M. E. M.: Presenting your structures: the CCP4mg molecular-graphics software, Acta Crystallogr. D, 67, 386–394, https://doi.org/10.1107/S0907444911007281, 2011. a
Orton, H. W. and Otting, G.: Accurate electron–nucleus distances from paramagnetic relaxation enhancements, J. Am. Chem. Soc., 140, 7688–7697, https://doi.org/10.1021/jacs.8b03858, 2018. a
Orton, H. W., Kuprov, I., Loh, C.-T., and Otting, G.: Using paramagnetism to slow down nuclear relaxation in protein NMR, J. Phys. Chem. Lett., 7, 4815–4818, https://doi.org/10.1021/acs.jpclett.6b02417, 2016. a, b, c, d, e
Orton, H. W.: Paramagpy source code, Version v1.0, Zenodo, https://doi.org/10.5281/zenodo.3594568, 2019. a, b
Pearce, B. J. G., Jabar, S., Loh, C.-T., Szabo, M., Graham, B., and Otting, G.: Structure restraints from heteronuclear pseudocontact shifts generated by lanthanide tags at two different sites, J. Biomol. NMR, 68, 19–32, https://doi.org/10.1007/s10858-017-0111-z, 2017. a
Pintacuda, G., Hohenthanner, K., Otting, G., and Müller, N.: Angular dependence of dipole-dipole-Curie-spin cross-correlation effects in high-spin and low-spin paramagnetic myoglobin, J. Biomol. NMR, 27, 115–135, https://doi.org/10.1023/A:1024926126239, 2003. a, b
Pintacuda, G., Kaikkonen, A., and Otting, G.: Modulation of the distance dependence of paramagnetic relaxation enhancements by CSA × DSA cross-correlation, J. Magn. Reson., 171, 233–243, https://doi.org/10.1016/j.jmr.2004.08.019, 2004a. a, b, c, d
Pintacuda, G., Keniry, M. A., Huber, T., Park, A. Y., Dixon, N. E., and Otting, G.: Fast structure-based assignment of 15N HSQC spectra of selectively 15N-labeled paramagnetic proteins, J. Am. Chem. Soc., 126, 2963–2970, https://doi.org/10.1021/ja039339m, 2004b. a
Raman, S., Lange, O. F., Rossi, P., Tyka, M., Wang, X., Aramini, J., Liu, G., Ramelot, T. A., Eletsky, A., Szyperski, T., Kennedy, M. A., Prestegard, J., Montelione, G. T., and Baker, D.: NMR structure determination for larger proteins using backbone-only data, Science, 327, 1014–1018, https://doi.org/10.1126/science.1183649, 2010. a
Rinaldelli, M., Carlon, A., Ravera, E., Parigi, G., and Luchinat, C.: FANTEN: a new web-based interface for the analysis of magnetic anisotropy-induced NMR data, J. Biomol. NMR, 61, 21–34, https://doi.org/10.1007/s10858-014-9877-4, 2015. a
Schmitz, C., Stanton-Cook, M. J., Su, X.-C., Otting, G., and Huber, T.: Numbat: an interactive software tool for fitting Δχ-tensors to molecular coordinates using pseudocontact shifts, J. Biomol. NMR, 41, 179–189, https://doi.org/10.1007/s10858-008-9249-z, 2008. a, b, c
Schmitz, C., Vernon, R., Otting, G., Baker, D., and Huber, T.: Protein structure determination from pseudocontact shifts using ROSETTA, J. Mol. Biol., 416, 668–677, https://doi.org/10.1016/j.jmb.2011.12.056, 2012. a, b, c
Schrödinger, LLC: The PyMOL molecular graphics system, version 1.8, 2015. a
Solomon, I.: Relaxation processes in a system of two spins, Phys. Rev., 99, 559–565, https://doi.org/10.1103/PhysRev.99.559, 1955. a, b
Stanton-Cook, M. J., Su, X.-C., Otting, G., and Huber, T.: PyParaTools, available at: http://comp-bio.anu.edu.au/mscook/PPT/ (last accees: 15 October 2019), 2014. a
Suturina, E. A., Mason, K., Geraldes, C. F. G. C., Chilton, N. F., Parker, D., and Kuprov, I.: Lanthanide-induced relaxation anisotropy, Phys. Chem. Chem. Phys., 20, 17676–17686, https://doi.org/10.1039/C8CP01332B, 2018. a, b, c
Valafar, H. and Prestegard, J. H.: REDCAT: a residual dipolar coupling analysis tool, J. Magn. Reson., 167, 228–241, https://doi.org/10.1016/j.jmr.2003.12.012, 2004. a, b
Vega, A. J. and Fiat, D.: Nuclear relaxation processes of paramagnetic complexes the slow-motion case, Mol. Phys., 31, 347–355, https://doi.org/10.1080/00268977600100261, 1976. a
Vranken, W. F., Boucher, W., Stevens, T. J., Fogh, R. H., Pajon, A., Llinas, M., Ulrich, E. L., Markley, J. L., Ionides, J., and Laue, E. D.: The CCPN data model for NMR spectroscopy: development of a software pipeline, Proteins, 59, 687–696, https://doi.org/10.1002/prot.20449, 2005. a
Zweckstetter, M. and Bax, A.: Prediction of sterically induced alignment in a dilute liquid crystalline phase: aid to protein structure determination by NMR, J. Am. Chem. Soc., 122, 3791–3792, https://doi.org/10.1021/ja0000908, 2000. a
- Abstract
- Introduction
- Pseudocontact shifts
- Residual dipolar couplings
- Paramagnetic relaxation enhancements
- Curie-spin dipole–dipole cross-correlated relaxation
- Uncertainty calculations
- Molecular structures with multiple models
- Quality factors
- Graphical user interface
- Visualisation
- Scripting
- NMR software integration
- Tensor conventions and conversions
- Example PRE calculation
- Conclusions
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement
- Abstract
- Introduction
- Pseudocontact shifts
- Residual dipolar couplings
- Paramagnetic relaxation enhancements
- Curie-spin dipole–dipole cross-correlated relaxation
- Uncertainty calculations
- Molecular structures with multiple models
- Quality factors
- Graphical user interface
- Visualisation
- Scripting
- NMR software integration
- Tensor conventions and conversions
- Example PRE calculation
- Conclusions
- Code availability
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Supplement





